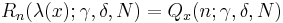Dual Hahn polynomials

In mathematics, the dual Hahn polynomials are a family of orthogonal polynomials in the Askey scheme of hypergeometric orthogonal polynomials. They are defined in terms of generalized hypergeometric functions by

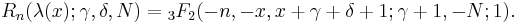$R_n(\lambda(x);\gamma,\delta,N)= {}_3F_2(-n,-x,x%2B\gamma%2B\delta%2B1;\gamma%2B1,-N;1).\$ for 0≤n≤N

where λ(x)=x(x+γ+δ+1).

Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.

Closely related polynomials include the Hahn polynomials, the continuous Hahn polynomials p_n(x,a,b, a, b), and the continuous dual Hahn polynomials S_n(x;a,b,c). These polynomials all have q-analogs with an extra parameter q, such as the q-Hahn polynomials Q_n(x;α,β, N;q), and so on.

Orthogonality

Dual Hahn polynomials are related to Hahn polynomials Q by switching the roles of x and n: more precisely

$R_n(\lambda(x);\gamma,\delta,N) = Q_x(n;\gamma,\delta,N)$

Racah polynomials are a generalization of dual Hahn polynomials

Hahn, Wolfgang (1949), "Über Orthogonalpolynome, die q-Differenzengleichungen genügen", Mathematische Nachrichten 2: 4–34, doi:10.1002/mana.19490020103, ISSN 0025-584X, MR 0030647
Koekoek, Roelof; Lesky, Peter A.; Swarttouw, René F. (2010), Hypergeometric orthogonal polynomials and their q-analogues, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-642-05014-5, ISBN 978-3-642-05013-8, MR 2656096
Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Hahn Class: Definitions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248, http://dlmf.nist.gov/18.19